Low-rank Adaptation

Large language models, as the name already states, have a huge quantity of parameters and have been trained on large-scale datasets to obtain excellent generalization capabilities.

But if it's so good, why would people want to modify such models?
1. To have a specific behavior - Let's say you have a company that sells bikes, and you want to create a chatbot to deal with some customer services. The most efficient way of doing so would be to finetune a large language model - so that it preserves the knowledge it already had but now acts like a real team member of your company willing to solve costumer's problems.
2. To improve the performance - The large language model isn't very good for your native language. By finetuning it, you could improve the model's knowledge and avoid mistakes. For security reasons - if you have a well-trained model and want to prevent it from generating harmful content, you can run a 'safety' finetuning so that the model is less likely to produce this kind of material;

The problem is that even finetuning (which is usually faster than pretraining the models) is a very memory-consuming task due to the number of parameters these models have. Some techniques to overcome that, such as freezing parts of the model to avoid computing gradients from them, therefore, saving memory, or adding layers on top of the model while freezing the whole rest, were a lot used in the past but usually come with either accuracy or speed harm; This is where LoRa comes into play. LoRa is a well-known technique that aims at reducing the training time by being parameter-efficient.

How does LoRa work?

LoRa works by creating smaller matrices to train and, therefore, requires less memory and time to train. But if we add more matrices (i.e., linear layers), wouldn't the inference time increase? Not really. These matrices are elaborated with dimensions that merging them into the original model possible.

First, let's see why it is memory efficient. Consider you have an attention-based model if you have 32 encoder blocks, and considering that each block has a single multi-head attention layer and therefore four matrices (Wq, Wk, Wv, and Wo), we end up with 128 matrices.

If the matrices hold 1280x1280 dimensions, each matrix will have 1.638.400 parameters. By multiplying this by for (since we have a query, key, value, and output matrices per encoder block), we have 6M parameters per encoder block - not even considering the rest of the layers. Scaling that up to the 32 encoder blocks we have, it is already a ~210M parameters model (and notice that this doesn't even include the decoder parts).

If we wanted to finetune this model without using LoRa, we would need to store gradients for each parameter - which consumes the same memory as the parameter itself, the optimizer states, the activations and still be able to store some data (batch size) into the GPU memory.

But with LoRa it would be a whole different story. LoRa relies on the fact that finetuning large models to specific tasks has a low intrinsic rank due to a huge redundancy over the parameter matrices. Rank in linear algebra refers to the maximum number of linearly independent column vectors in the matrix, and a matrix is said to be full-rank if the smallest dimension of the matrix is equal to its rank.

Consider you have an attention matrix with dimensions of 1280 x 1280. Multiplying the two, would end up with 1.6M parameters. Let's then create two other matrices with rank 8.

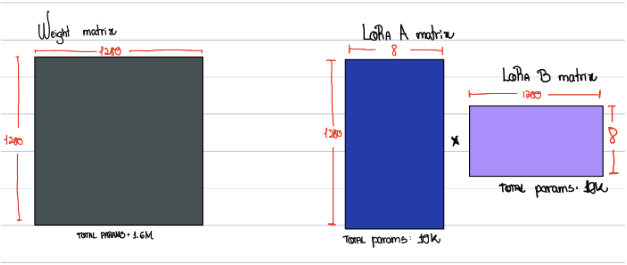
In the left matrix (represented by the grey square) we have 1.6M parameters to tune (1280 x 1280). However, on the right, we end up with only 20k parameters (summing both LoRa A and LoRa B matrices). If we multiply the two LoRa matrices, we end up with a 1280 x 1280 dimension matrix, which matches the original one mentioned previously that holds 1.6M parameters.

Notice that our model will be using both to compute the forward method:

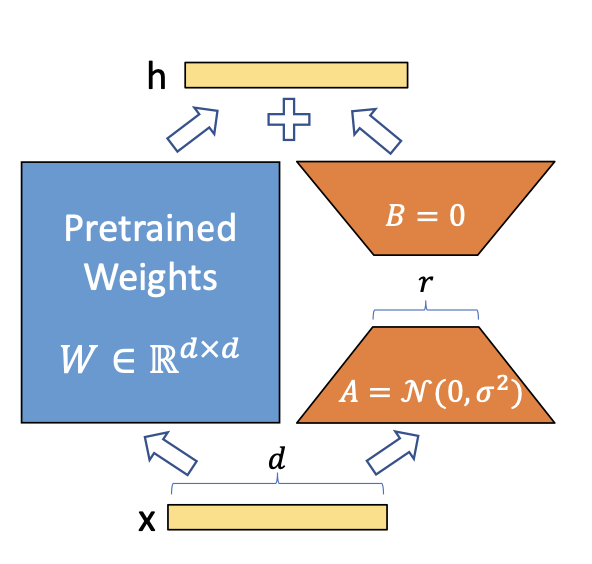
Given an input X, we freeze the left matrix not to waste memory computing its gradients. We multiply X by W and meanwhile multiply it by AB and sum the result. As described in the equation below:

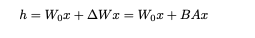
This way we only store gradients and activations for LoRa matrices. But if we add new parts to the model, isn't it going to slow down inference? Not really. Due to the dimensions matching on both matrices W and AB, we can sum them up into the original layer and preserve the capabilities of the new fine-tuned model. Just like this:

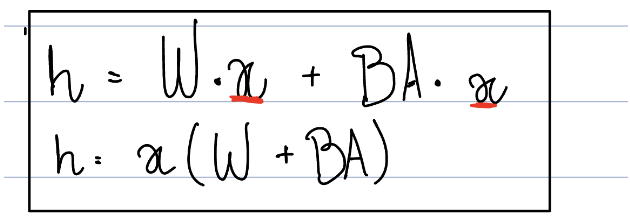
How to choose the rank size?

The authors claim that a good approach for this is to start with big ranks (which would be similar as a regular finetuning) and then decrease the rank gradually until the model stops learning.

This technique is often used if you plan to have multiple models (each acting differently). You can quickly finetune multiple LoRa matrices and change the model accordingly to the behavior you'd like it to have. Let's say you have a language model that doesn't perform properly in Portuguese and German. You can train two separate adapter layers for them and use them if the user wants to talk in Portuguese. Or keep the original weights if the user is writing in English.

Share on: