Enhancing AI Alignment with Direct Preference Optimization

Aligning models to human values and desires is a formidable task, particularly when we're working with vast datasets that resist meticulous control. Concerns arise when language models spew out content that could be false or harmful. Luckily, advancements in AI research are opening pathways for safer and more reliable interactions with these systems.

One spotlight fix is the leap from GPT-3 to ChatGPT, which captured the imaginations of many by actively aligning outputs with user preferences. This leap relied on a technique known as reinforcement learning.

Let's revisit the steps behind Reinforcement Learning from Human Feedback (RLHF):
1. Supervised Fine-Tuning (SFT): We begin by refining our extensive language model with copious amounts of data. Consider this a formative stage where the model gets the bulk of its knowledge.
2. Training a Reward Model based on Human Preferences: Next, we probe the SFT model with scenarios, presenting human evaluators with pairs of model-generated responses to label one as preferable. The data compiles into a set of triplets: D = {x, y_preferred, y_not_preferred} to guide the model's learning. The aim here is to train the model to differentiate between a 'preferred' response and its counterpart. We strive to maximize the difference between the reward scores for each, ensuring the model can identify what humans are more likely to value.

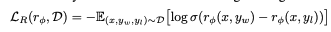
We want to maximize the distance between r(x,y_winner) - i.e., how likely the preferred output is to be tagged as so and r(x,y_looser). The reward model is usually the SFT (from the 1st step) with a linear layer on top of it (so that it becomes a classification model).

1. RL finetuning phase: After having the reward model predict correctly if a completion is appropriate or not, we need to incorporate that into our final finetuning step, which is described as the following:

Adapt my language model so that it matches human preferences (mimicked by the reward model) but without losing too much of the capabilities of my initial SFT model - so that we don't fall into a poorly performant model and also a reward hacking model. The optimization problem to be solved is this:

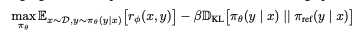
• r(x,y) is our reward model;
• Pi0 is the current RLHF model (the one being trained in this step)
• PiRef is the SFT model (trained on the initial phase)
• B is a parameter that indicates how much the deviation between the SFT and RLHF model is going to

Our end goal is that the model reward for this is high and that the KL divergence is not very large, indicating a big shift between the two distributions. This specific optimization problem is not differentiable due to the nature of language model generation, so the standard approach has been to construct the reward function as follows:

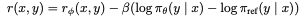
Now that we have seen the expensive pipeline associated with RLHF let's look into DPO, which will maintain the main properties of RLHF models (aligned to human preferences) without the need to use reinforcement learning. DPO reduces reward model fitting and reinforcement learning into a single maximum likelihood objective while maintaining and even improving the capabilities brought by RLHF. The paper's name gives us a clue about the intuition behind the technique: 'Your language model is secretly a reward model.'. It relies on the model's capabilities of understanding which completions are 'human preferred' and which are not.

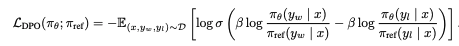
The intuition behind the proposed loss function is relatively simple: We want the current model (Pi0) to give us a higher probability for the winner sequence (Yw), and the current model (Pi0) assigns a lower probability to the loser sequence. The division serves as a regularization to stay consistent with the original distribution and prevent the model from reward hacking - just as we saw in the original RLHF formula. Notice that there's no binary classification problem and that instead, we are now using the language model to identify the conditional probabilities given a sequence.

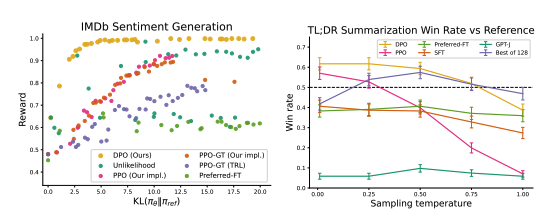
The results on the left show that DPO achieves higher expected rewards for all KL divergence values between the Pi0 and the PiRef models, and the results on the right show that it is more robust in changes over the sampling temperatures.

Share on: